Login or Create an Account to view question mark schemes (answers), comment, and download a PDF of this test
Question 1[5 Marks]
Given a 2D array called ARR of size 4x3 and an empty 1D array called BIGGEST of size 4, construct an algorithm to sequentially fill BIGGEST with the biggest number in each ARR row such that the index of each number in BIGGEST is the same as its original ARR row index.
The more positive or less negative a number, the bigger it is - for example, 7, 0 and -2 are all considered bigger than -10.
ARR may contain one or more negative numbers.
For example, consider the following 2D array:
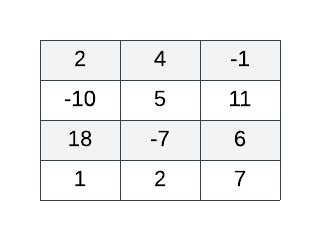
The correctly functioning algorithm applied to the 2D array above yields the following 1D array:
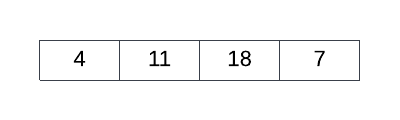
Question 2[12 Marks]
At the moment marathon runners cross the finishing line of a race, their names are added to a stack called RUNNERS.
For example, a diagram of RUNNERS below indicates “Ellie” has finished first and “Jessie” last. “Jessie” is at the top of the RUNNERS stack.
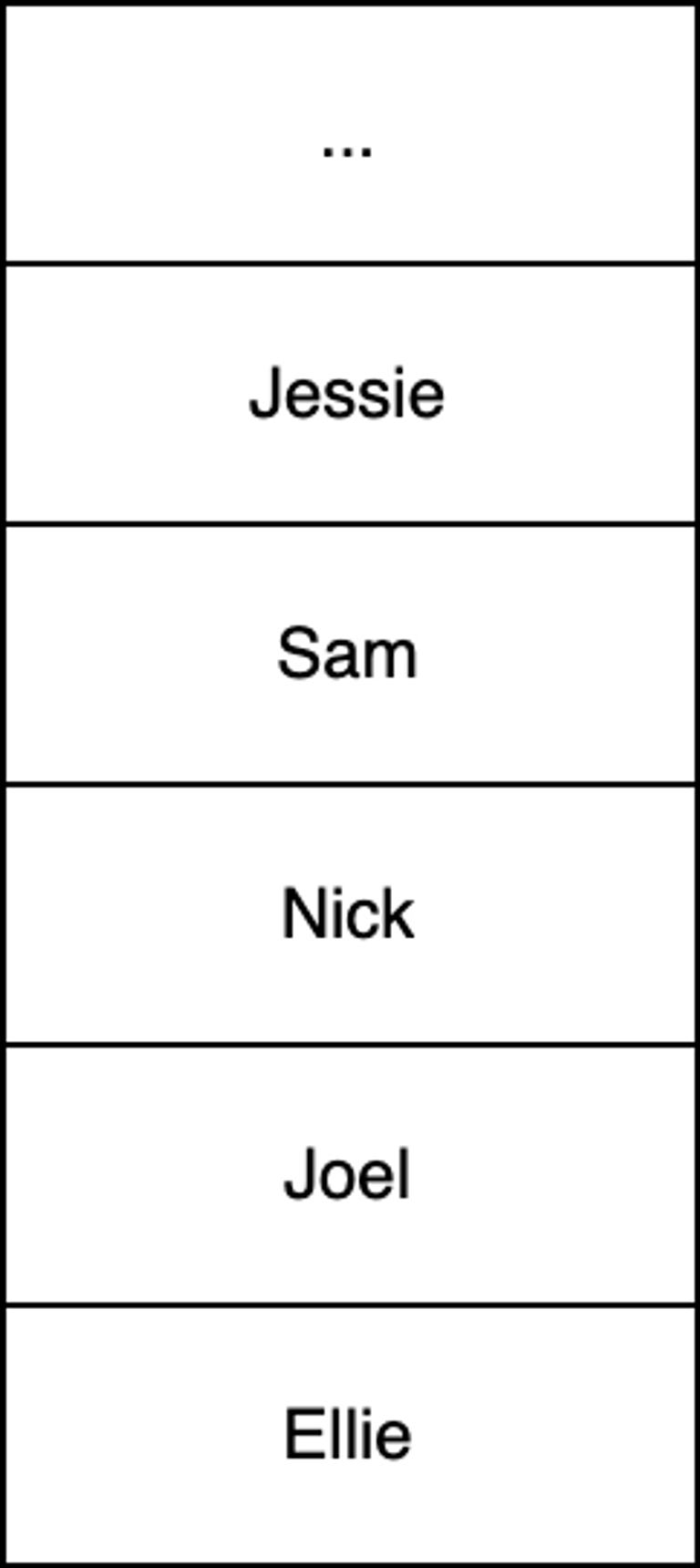
(a).
Using pseudocode, construct an efficient procedure that will search the stack RUNNERS for a name given via standard input. Once the given name is found, output the finishing place of the runner specified as a number. If a name is not found then the procedure should output the message "Runner not found".
Assume all names are unique, the number of elements in RUNNERS is unknown and RUNNERS may be emptied during the search process.
[6]For example, given an input string of "Joel" the procedure will output the number 2 to indicate Joel finished in 2nd place.
(b).
Outline why the use of a queue would make this algorithm simpler and more efficient than using a stack.
[2]In the same way as RUNNERS saves each runner's name, another stack called TIMES saves each runner's finishing time as they cross the finish line.
(c).
The results of a particular competition where 101 runners successfully finish a race are held in RUNNERS and TIMES. Given an empty 101x2 (row x column) 2D array called RESULTS, write pseudocode such that the first column contains the names of all those runners who finished the race and the second column contains their respective times in ascending rank order.
[3]For example, RESULTS[7][1] should contain the time of the runner who finished in 94th place, that is, having only ran faster than seven people (eighth last).
(d).
Using RESULTS, state the single line of pseudocode that represents the name of the runner with the median finishing time.
[1]Question 3[4 Marks]
Construct an algorithm using an empty stack called STACK to reverse an array containing 7 elements called ARRAY.
Question 4[5 Marks]
Consider the following algorithm.
function fun(N)
if N = 0 then
return 1
else if (N % 2 == 0)
return N - fun(N-1)
else
return N + 2 × fun(N-1)
end if
end function
(a).
State what would occur if the first "if statement" were removed.
[1](b).
Trace the algorithm when N=4 by completing the following trace table.
[3]N | fun(N) returns
-------------------
4 |
3 |
2 |
1 |
0 |
(c).
State the final output of the algorithm when N=4.
[1]Question 5[14 Marks]
Consider the following diagram representing seats in a movie theater where each seat is specified by a row number ranging from 1 to 7 (inclusive) and a column number ranging from 1 to 10 (inclusive).
The theater's ticketing system has already allocated Andrew ("A"), Sally ("S") and Rufus ("R") seats for an upcoming screening.
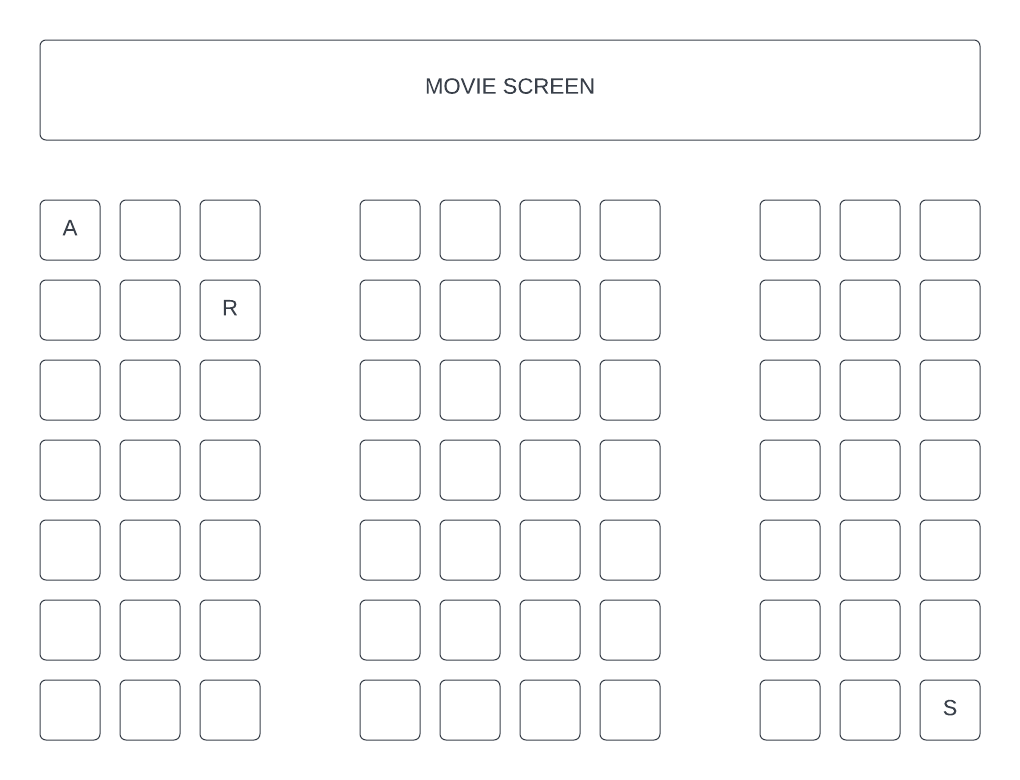
The ticketing system stores ticketing information in a collection called TICKETS.
TICKETS is composed of nodes where values alternate between integers and strings - each integer has encoded seating information for the customer whose name is held as a string in the next node. The first two digits and the last two digits of each integer specify the row number and column number of a seat respectively. For example, Rufus has a ticket for the third seat across in the second row.
TICKETS contains only those customers with a ticket and all ticket holders have exactly one allocated seat each. In TICKETS, it can be assume that a customer name will always follow their seating number. Therefore, customer seating information is always held in sequentially linked pairs - for example:

(a).
Construct an algorithm to only output all ticket holder names held in TICKETS.
[4](b).
Describe one problem with storing ticketing information in this way and explain why a 2D array would be more appropriate.
[3](c).
Given a 7x10 2D array called TIX, construct an algorithm to parse ticketing information from the collection TICKETS into TIX such that ticket holder names are copied to a TIX location representative of their seat location. For example, TIX[0][0], TIX[1][2], and TIX[6][9] should hold the names "Andrew", "Rufas" and "Sally" respectively.
Unassigned seats should be indicated in TIX by the string "Empty".
[7]Question 6[3 Marks]
Contrast the use of a linked list with an array for capturing streaming measurements from a weather station hygrometer (a device which measures humidity).
Question 7[6 Marks]
(a).
State what is meant by the term ‘dynamic data structure’
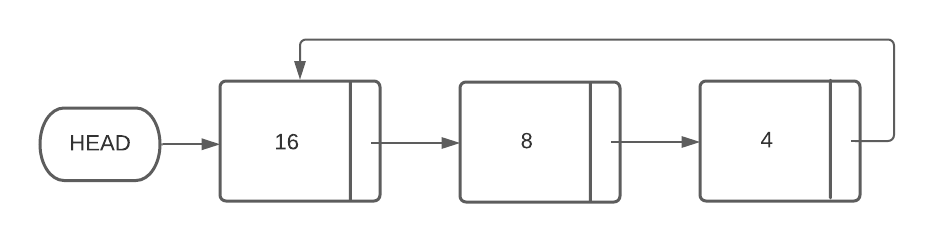
[1]Consider the following circularly linked list
(b).
Given a new node containing the number 7 (called NEW_NODE) and a pointer (called PREV_NODE) which points to the node containing the number 8, describe how the new node should be added to the linked list in such a way that the circularly linked list remains both properly formed and sorted.
[3](c).
In contrast to the process described in part b), outline why it would be less efficient to add the value 32 to a static array containing [16, 8, 4] in such as way as to preserve both existing values and ascending order.
[2]Question 8[11 Marks]
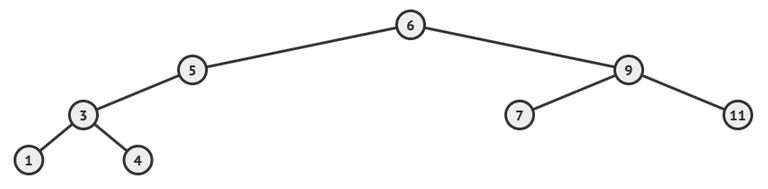
(a).
With respect to the binary search tree above, list all the nodes values according to the order in which they are visited by the following tree traversals.
(i).
In-order
[1](ii).
Pre-order
[1](iii).
Post-order
[1](b).
Describe how the post-order tree traversal algorithm works.
[3](c).
In contrast to arrays, outline two benefits of using binary search trees.
[4](d).
In contrast to a balanced binary search tree, identify one disadvantage of an unbalanced binary search tree;
[1]Question 9[7 Marks]
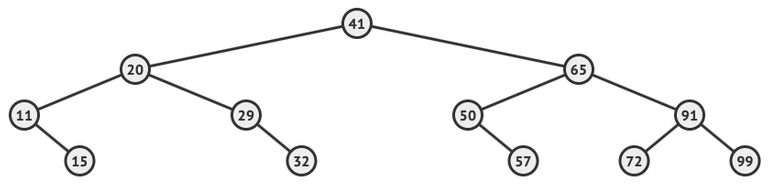
In consideration of the binary tree shown above
(a).
State the value contained in each of the following:
(i).
The root node
[1](ii).
The last node visited by an pre-order traversal
[1](iii).
The leaves of the largest possible left subtree
[2](iv).
The right child of the sibling of the node containing 65
[1](b).
Draw a resulting tree if the node containing the value 65 were removed
[2]9 Questions67 MarksPremium
60 Uses1417 Views1 Like