Ahead of the Stack
Extended Response12 MarksPremium
At the moment marathon runners cross the finishing line of a race, their names are added to a stack called RUNNERS.
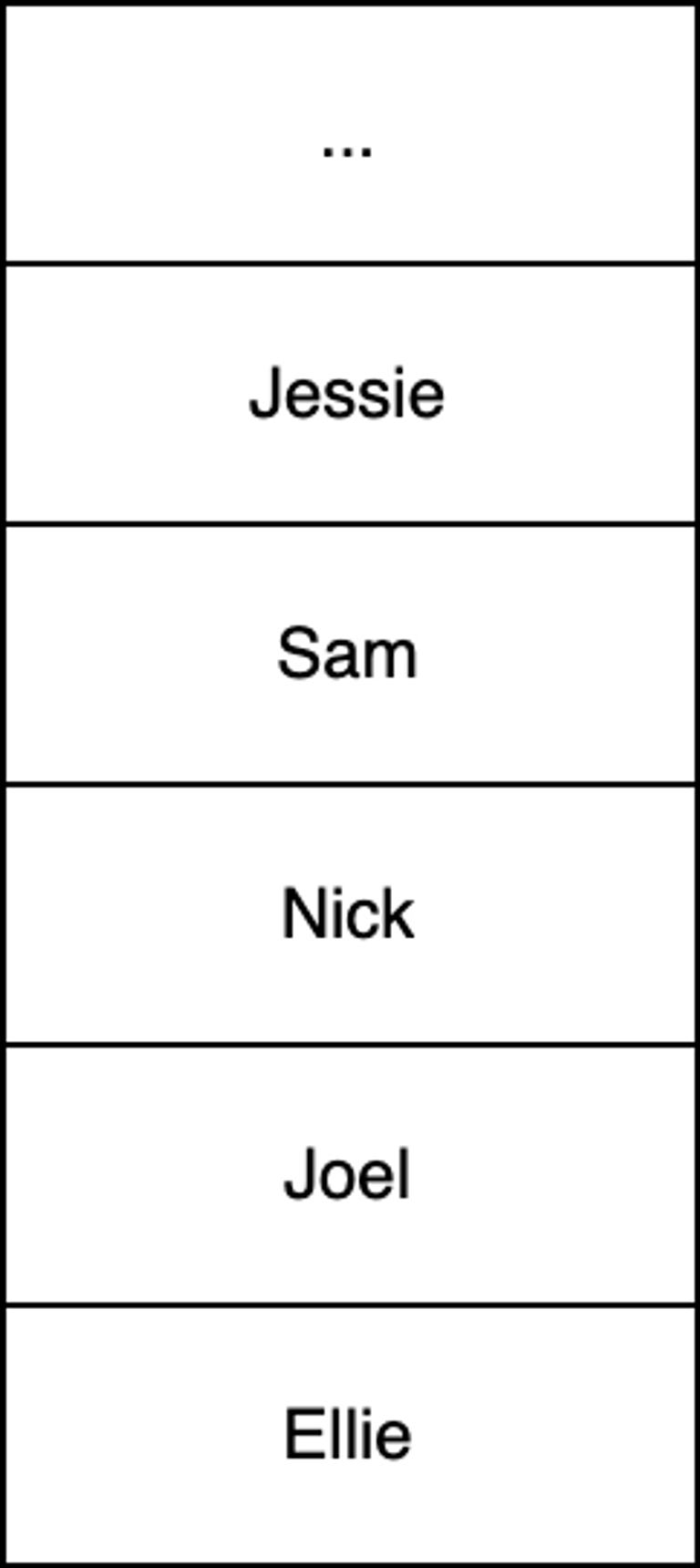
For example, a diagram of RUNNERS below indicates “Ellie” has finished first and “Jessie” last. “Jessie” is at the top of the RUNNERS stack.
(a).
Using pseudocode, construct an efficient procedure that will search the stack RUNNERS for a name given via standard input. Once the given name is found, output the finishing place of the runner specified as a number. If a name is not found then the procedure should output the message "Runner not found".
Assume all names are unique, the number of elements in RUNNERS is unknown and RUNNERS may be emptied during the search process.
[6]For example, given an input string of "Joel" the procedure will output the number 2 to indicate Joel finished in 2nd place.
(b).
Outline why the use of a queue would make this algorithm simpler and more efficient than using a stack.
[2]In the same way as RUNNERS saves each runner's name, another stack called TIMES saves each runner's finishing time as they cross the finish line.
(c).
The results of a particular competition where 101 runners successfully finish a race are held in RUNNERS and TIMES. Given an empty 101x2 (row x column) 2D array called RESULTS, write pseudocode such that the first column contains the names of all those runners who finished the race and the second column contains their respective times in ascending rank order.
[3]For example, RESULTS[7][1] should contain the time of the runner who finished in 94th place, that is, having only ran faster than seven people (eighth last).
(d).
Using RESULTS, state the single line of pseudocode that represents the name of the runner with the median finishing time.
[1]Looping Lists
Extended Response16 MarksPremium
(a).
Using the table below as a guide, trace the following algorithm by filling out the trace table below row by row (left to right).
[4]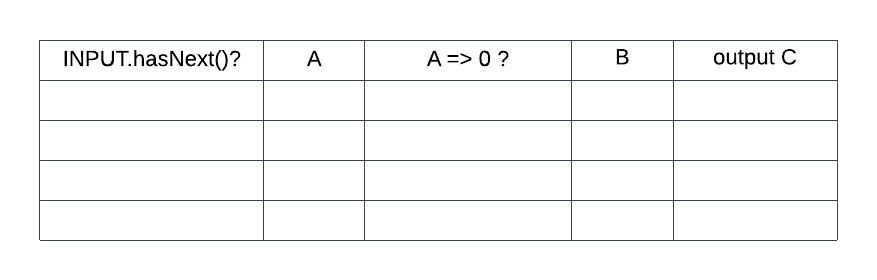
INPUT = [2, -2, -5, 7, 0] // A collection
A=0
B=0
C=0
loop while INPUT.hasNext()
A = INPUT.getnext()
if (A => 0) then
B = INPUT.getnext()
end if
C = A+B
output C
end loop
(b).
Explain why binary search is almost always more efficient than linear search on ordered values.
[4](c).
In the context of programming, define a flag.
[1](d).
Given two arrays, ALPHA which contains 10 elements and BETA which contains 20 elements, construct an algorithm to determine whether or not ALPHA is a subset of BETA. That is, if all the items in ALPHA are also in BETA then output “SUBSET” otherwise output “NOT SUBSET”
[7]